Sulla divulgazione
A volte mi infilo per sbaglio in delle discussioni che alcuni vogliono chiamare divulgative, ben sapendo di essere un pessimo divulgatore. E il risultato e' che alla fine mi trovo a scrivere cose che hanno senso, ma solo a patto di sapere altre cose. Altrimenti sono sbagliate. E questo non succede solo in campi dubbi, ma anche in campi esatti per eccellenza , come la matematica.
Alla matematica vengono attibuiti diversi poteri magici, tra cui quello di essere a-storica, ovvero quello di rappresentare delle verita' che sono quelle, sono sempre state quelle, e saranno sempre quelle. Verissimo.
Il problema e' che “la matematica ha una storia” fa si' che la formulazione della matematica cambi nel tempo. Faccio un esempio: il numero “1” e' un numero primo?
Eh. La risposta corretta e' che esiste una formulazione moderna attorno agli anni 1850 che stabilisce chiaramente che 1 non è un numero primo.
Questa formulazione è attribuita al matematico tedesco Peter Gustav Lejeune Dirichlet (1805-1859), che nel 1837 fornì una definizione rigorosa di numero primo che esclude esplicitamente 1:
Un numero primo è un numero intero positivo maggiore di 1 che è divisibile solo per 1 e se stesso.
Questa definizione, che è tuttora ampiamente accettata nella teoria dei numeri moderna, afferma in modo inequivocabile che 1 non può essere considerato un numero primo, in quanto non soddisfa il requisito di avere esattamente due divisori distinti (1 e se stesso).
Dirichlet consolidò così la nozione introdotta da Euclide secoli prima, fornendo una definizione precisa e rigorosa di numero primo che rimuove ogni ambiguità sullo status di 1 come non-primo.
Quindi si, piu' o meno, ma la dimostrazione di Euclide (circa il 300 AC) non sarebbe accettata oggi, perche' usava delle definizioni abbastanza strane: Euclide considerava , per ragioni filosofiche, l'unita' come un caso a parte, una cosa speciale , e quindi la sua “dimostrazione” consisteva nel definire i numeri primi togliendo il numero uno. Punto. Non e' un numero primo perche' lo dice Euclide, e Euclide lo dice perche' trova affascinante il concetto di unita'. Punto.
Se andiamo ai numeri reali, che furono oggetto della discussione, la cosa e' ancora peggiore.
La prima cosa da notare e' che nessuno hai mai visto, nel mondo fisico, un numero reale. Ogni numero che viene usato in sede pratica , o sperimentale, o misurativa, ha una quantita' limitata di “numeri a destra della virgola”. Questo fa in modo che di fatto l'insieme dei razionali potrebbe contenere tutti i numeri che realmente usiamo, dal momento che qualsiasi misura ha un errore, che si traduce di fatto in un errore di troncatura. I fisici danno un limite convenzionale (l'esperimento ha funzionato a meno di un errore piu' piccolo di cinque sigma), e se ne fregano.
Dimenticando pero' che cosi' facendo, qualsiasi risultato sara' anche membro dell'insieme dei numeri razionali. Se vogliamo dire “radice di due” o “pigreco” dobbiamo dire che e' un numero reale. Ma se misuriamo la diagonale di un quadrato, o la circonferenza di un cerchio, otteniamo sembre un numero che sappiamo dovrebbe essere in R, ma puo' essere contenuto in Q, per via della troncatura. 3,5 e' 35/10, che e' razionale. 1.4242135 , la troncatuira della radice di 2, e' ancora razionale: 14142135/10000000 .
I fisici, cioe', usano i numeri reali di continuo (differenziare e' l'esempio tipico) , ma non hanno mai davvero visto in laboratorio un insieme infinito, e nemmeno un insieme continuo. I numeri che maneggiano davvero sono razionali, e sia gli irrazionali che i trascendenti sono troncati dall'operazione di “misura” , ovvero ancora razionali. E non migliorera' certo usando i computer, che sono macchine discrete.
Perche' siamo a questo punto? occorre capire che anche i numeri reali hanno una storia.
La loro formulazione in termini matematici potrebbe essere scritta cosi':

Che, in un linguaggio naturale un po' approssimativo, posso descrivere cosi':
Gli assiomi fondamentali per costruire l'insieme dei numeri reali R sono i seguenti:
Assiomi di campo
Assioma di chiusura per l'addizione: Per ogni coppia di numeri reali a e b, la loro somma a + b è un numero reale.
Assioma di esistenza dell'elemento neutro per l'addizione: Esiste un unico numero reale, indicato con 0, tale che per ogni numero reale a, si ha a + 0 = a.
Assioma di esistenza dell'opposto: Per ogni numero reale a, esiste un unico numero reale -a tale che a + (-a) = 0.
Assioma di chiusura per la moltiplicazione: Per ogni coppia di numeri reali a e b, il loro prodotto a · b è un numero reale.
Assioma di esistenza dell'elemento neutro per la moltiplicazione: Esiste un unico numero reale, indicato con 1, diverso da 0, tale che per ogni numero reale a, si ha a · 1 = a.
Assioma di esistenza dell'inverso per la moltiplicazione: Per ogni numero reale a ≠ 0, esiste un unico numero reale 1/a tale che a · 1/a = 1.
Assiomi di associatività, commutativià e distributività per le operazioni di addizione e moltiplicazione.
Assiomi dell'ordine
Assioma di tricotomia: Per ogni coppia di numeri reali a e b, vale una e una sola delle seguenti relazioni: a < b, a = b, a > b.
Assioma di transitività: Se a < b e b < c, allora a < c.
Assioma di completezza
- Assioma di completezza o assioma di Dedekind: Ogni sottoinsieme non vuoto dei numeri reali che è superiormente limitato ammette un estremo superiore.
Questi assiomi, insieme alle proprietà derivanti, caratterizzano completamente l'insieme dei numeri reali R e permettono di costruirlo a partire dai numeri razionali Q mediante il procedimento delle sezioni di Dedekind.
Tutto molto bello, ma... e prima che nascesse Dedekind?
Siccome definire i reali in primo ordine (logica di primo ordine) era una difficolta' insormontabile, vi poteva succedere che l'assioma numero 10 fosse abbastanza oscuro: avete presente quando si alza lo studente al liceo e chiede “ma prof, zero virgola nove periodico e uno sono lo stesso numero, si o no?”
Ecco, a questa domanda non era semplicissimo rispondere prima di un certo momento, perche' (blablabla Lemma di Zorn blablabla Logiche di secondo ordine blablabla) non erano ancora stati scritti certi libri. Poi arriva Dedekind e adesso abbiamo una risposta chiara: “ma chi cazzo credi di essere, Zorn?”.
Nonostante il fatto che con le formulazioni “antiche” si potessero fare calcoli ma non ci fosse nemmeno un ordinamento perfetto, ad un certo punto arriva Dedekind e abbiamo l'ordinamento perfetto.
(in realta' la storia e' diventata piu' complicata, Cantor ci e' diventato – letteralmente – matto, eccetera. )
Ma tutta questa gente che usava i reali a sproposito , e otteneva dei razionali, ma gli sembravano reali, non si accorgeva di tutta sta roba?
No. Tanto comunque, al fine pratico, loro avevano dei razionali. Ma stavano usando una matematica passata.
Perche' e' fondamentale?
Immaginiamo di sparare Einstein nell'antica Grecia. Vi presento il filosofo Monolito. E il filosofo greco Monolito si fa la sua teoria della relativita', ponendosi domande sui fulmini di Zeus. (i greci hanno fatto cose anche piu' stravaganti, quindi ci sta).
Arrivato alla teoria della relativita', arriva l'equazione di campo.
In determinate condizioni, come ad esempio in presenza di masse molto dense, le soluzioni di queste equazioni prevedono l'esistenza di singolarità, punti in cui la curvatura dello spazio-tempo diventa infinita. La singolarità del Big Bang iniziale e quelle presenti all'interno dei buchi neri sono esempi di tali singolarità previste dalla relatività generale .
Il nostro Monolito le guarda, ci pensa un pochino, e dice:
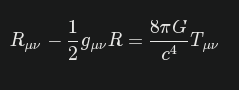
E dice: “ehi, ma li' c'e' Pi. E sappiamo bene che quel numero non esiste. Non e' un numero. Quindi la singolarita' esiste in un punto che non c'e'. Non esiste una singolarita', e' solo una delle infinite discontinuita' di Q. Non esistono punti cosi'. Quindi, siccome gli egizi hanno inventato la birra, vado a scolarmene una” nella kneippè (*) di sotto. “
E dico sul serio, per il greco Monolito quel punto non esisteva proprio. Per lui non succedeva niente in quel posto, era solo uno dei tanti buchi di Q. La continuita' non lo tangeva.
Morale:
sospetto che la fisica sarebbe molto diversa se alcune teorie fossero state fatte in passato, quando la matematica non era ancora “moderna”, e ho un sospetto altrettanto forte che i fisici si siano portati in casa molti guai, importandoli da alcune cose “complicate” come i numeri reali.
Non sono , ovviamente , l'unico che si e' chiesto se la fisica stia usando i numeri giusti. E neanche il primo. Hawkins, per dire, si fece la stessa domanda e provo' ad ipotizzare una dimensione temporale nel campo complesso. Anche lui, quindi, si chiese cosa succederebbe a cambiare numeri.
Ma il problema nello spiegarlo e' che ad un certo punto bisogna spiegare che senza Dedekind, e in un insieme di reali come quello fatto prima di Dedekind , che e' nato il 6 ottobre 1831, non aveva ordinamento perfetto.
Ma per spiegare , specialmente ai fisici, che tirandosi dentro delle scelte sui numeri da usare si sono tirati dentro assiomi a strafottere, non e' semplice. I topi di laboratorio ti rispondono “ma l'esperimento funziona, fottiti”, e quelli che si fanno chiamare “teorici” ti dicono “vabe', ma io sono un teorico, io mi riferisco ad un R teorico, mica devo misurare pigreco in laboratorio”.
Poi inciampano nelle singolarita', e Monolito il Greco se la ride dalla kneippè “L'egiziano”.
Ma il problema a divulgare questa cosa e' il rischio di scrivere delle cose che se investigate un pochino hanno senso, ma scritte cosi' sembrano assurde.
Anche perche' alcuni fisici rispondono: ehi, allora suggerisci tu un insieme da usare. Senza sapere che se fossi carogna, potrei suggerire i Numeri Surreali.
Che esistono:
https://it.wikipedia.org/wiki/Numero_surreale

(*) “kneippe” e' una parola tedesca, ma l'ho ellenizzata dando uno spirito alla e finale. Fottetevi pure.
Uriel Fanelli
Il blog e' visibile dal Fediverso facendo il follow a:
Contatti:
- Fediverse: @uriel@fedi.keinpfusch.net
- MATRIX: @uriel:mtrx.keinpfusch.net
- GNU JAMI: ufanelli